Laser Laboratory for Trace Analysis and Precision Measurements

Nobel Laureate in Physics John L. Hall once said, "Metrology is the mother of science." Wang Daheng, a key figure in China's "Two Bombs, One Satellite" project, also emphasized: "Metrology is the science of improving the precision of physical quantity measurements—it is both the foundation and the frontier of physics." The level of measurement technology not only influences scientific progress but also directly affects the order of societal functioning and a nation’s international standing. As early as 210 BC, Qin Shi Huang’s unification of weights and measures laid the foundation for over a millennium of prosperity in the Chinese nation and its position as a world power. Since the Industrial Revolution, Western countries have dominated the development of modern metrological standards and measurement technologies, thereby securing core influence in global trade, scientific and technological systems, and international regulations, while many developing countries have long remained at a disadvantage.

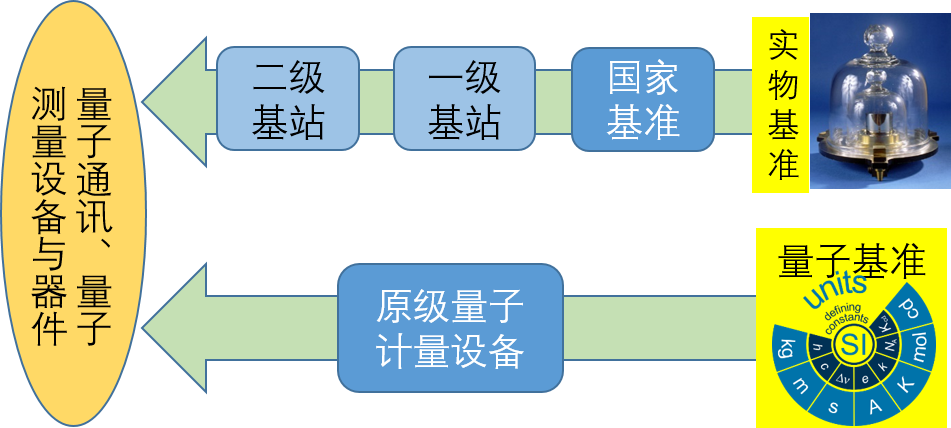
Currently, China still faces “bottleneck” challenges in high-precision metrological standards and core measurement technologies, which severely restrict independent innovation and international competitiveness across multiple industries. We are now at a critical juncture of historic transformation in the international metrology system—measurement standards are gradually shifting from traditional systems based on macroscopic artifacts to a “quantum standard” system centered on fundamental physical constants and quantum phenomena. Quantum metrology links unit definitions to fundamental physical constants and relies on quantum effects to realize measurement units, achieving “measurement as standard.” This drives high-precision, highly reliable, and traceable quantum measurement methods to become the mainstream direction of metrology development.

Fig. 1 Scientific Significance of Quantum Metrology

Optical Precision Measurement of Thermodynamic Temperature

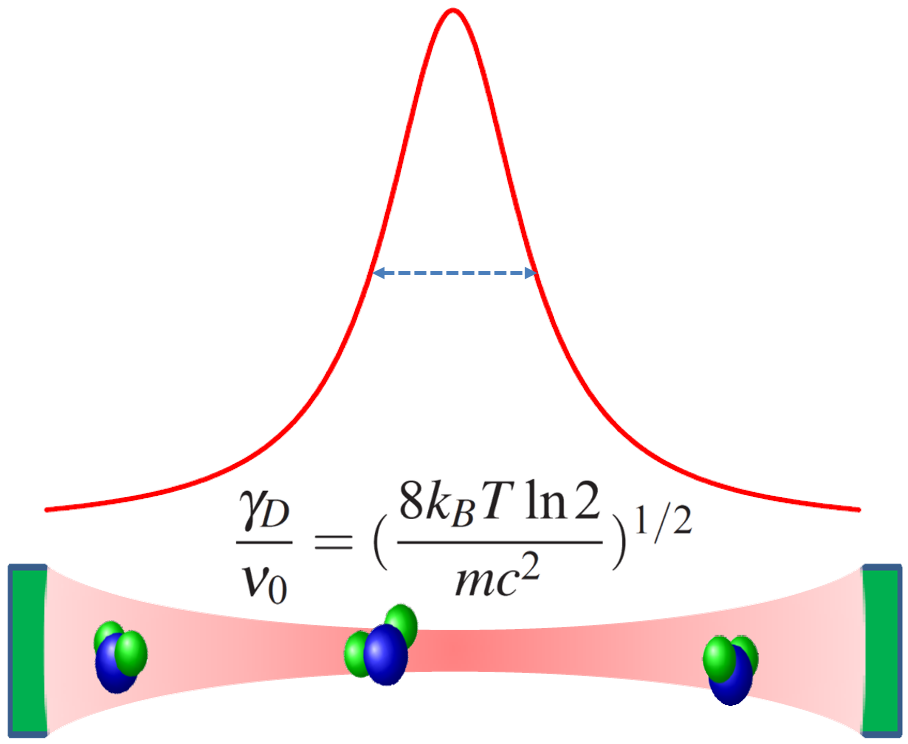
Accurate measurement of thermodynamic temperature plays a crucial role in scientific research, industrial manufacturing, aerospace, and other fields. Since the redefinition of the kelvin in the International System of Units (SI) from the water triple point to one based on the Boltzmann constant k_B, various absolute thermometry methods have been developed, such as acoustic gas thermometry (AGT) and Johnson noise thermometry (JNT). Our research group has long been dedicated to overcoming core quantum metrology technologies and has independently developed multiple spectroscopy-based thermodynamic temperature measurement methods, including Doppler broadening thermometry (DBT), line ratio thermometry (LRT), and refractive index gas thermometry (RIGT). Together, these form a promising system of optical thermometry techniques. Leveraging high-precision cavity-enhanced spectroscopy, our spectroscopic measurement system achieves a detection sensitivity of 10^-12/cm (equivalent to an optical path length of hundreds of kilometers), a spectral frequency precision at the kHz level, and a cavity mode stability at the sub-Hz level, along with milli-Kelvin temperature stability control. Based on this technology, we expect to achieve absolute gas temperature measurements at the parts-per-million (ppm) level. This approach not only offers a new high-precision temperature measurement solution but also demonstrates broad potential in molecular collision theory, detection of "forbidden" transitions, and trace gas sensing applications.

Fig. 3 Principles of Spectroscopic Measurement

Optical Traceable Measurement of Gas Pressure (Density)

As a fundamental physical quantity, the precise measurement of gas pressure has long relied on mercury manometers and mechanical piston gauges as national standards. In recent years, the emergence of optical vacuum metrology marks a significant shift from physical standards to quantum standards in pressure measurement. Our research group uses Fabry–Pérot cavities to achieve extremely high-precision measurements of the gas refractive index, from which gas density and pressure are derived. We have successfully developed China’s first experimental setup for absolute pressure measurement based on optical principles, overcoming multiple key technological challenges including precision laser frequency locking, high-stability cavity temperature control, and accurate optical frequency scanning and calibration. This method is expected to achieve pressure measurement accuracy at the ppm level and may evolve into a new national pressure standard, advancing pressure metrology into the quantum era.

Fig. 4 Schematic Diagram of Gas Pressure Measurement

Quantum Metrology and Standard Dissemination of Gas Concentration

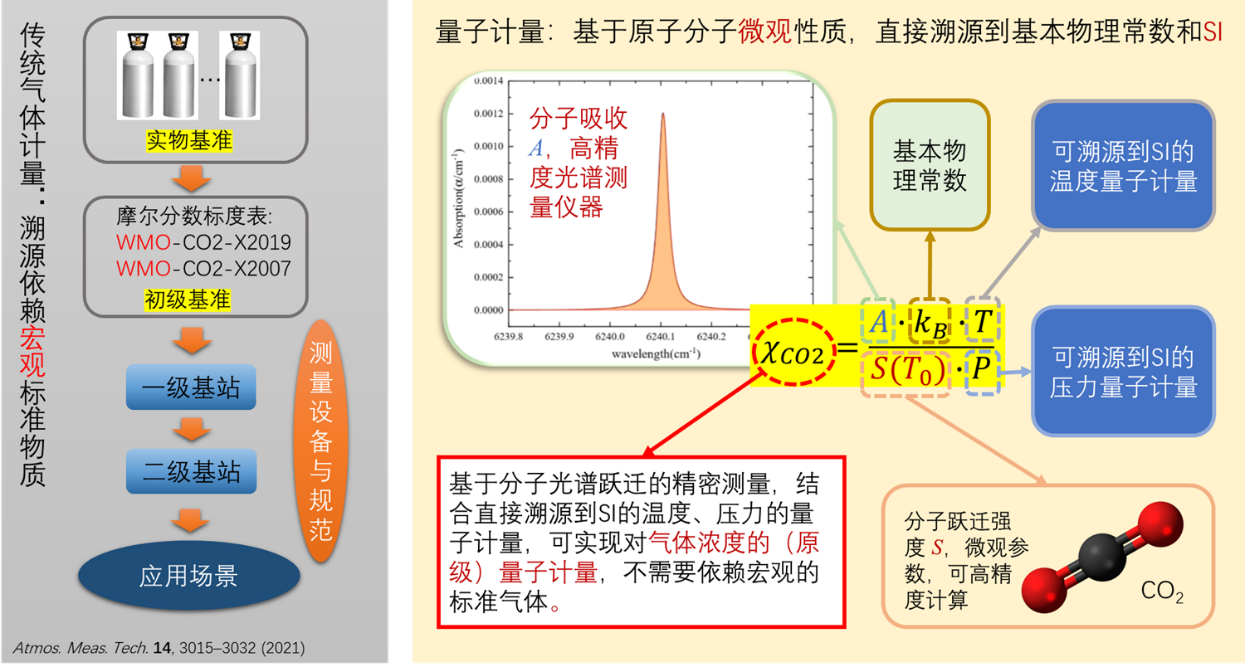
Gas concentration metrology aims to accurately determine the content of specific components in gas mixtures. This seemingly simple measurement profoundly impacts multiple critical fields, including environmental monitoring, public health, industrial production, and cutting-edge scientific research. For instance, in atmospheric greenhouse gas monitoring, isotope abundance analysis, toxic and hazardous gas detection, and medical diagnostics via breath analysis, the accuracy of concentration measurements directly affects policy formulation, safety assurance, and scientific credibility. Traditional gas concentration metrology primarily relies on gravimetric methods for preparing standard reference materials, which suffer from limited precision, complex value transfer, and difficulties in international comparison. Our research group has innovatively proposed spectroscopy-based methods for gas concentration metrology, directly tracing gas content back to physical constants and fundamental molecular parameters. This approach offers significant advantages, including independence from physical reference materials, high repeatability, and high precision. Specific research directions include: conducting high-precision measurements of absorption line intensities and intensity ratios for key atmospheric molecules such as CO and CO₂ and their isotopes; actively participating in international comparisons to promote the establishment of credible and traceable remote sensing data models for greenhouse gases; and ultimately developing a new generation of gas concentration calibration technologies and equipment traceable to the SI, serving national strategies such as carbon peak and neutrality and major atmospheric monitoring needs.

Fig. 5 The scientific significance of gas measurement